[10000印刷√] 二項定理 公式 三項 302358-二項定理 公式 三項

条件演算子は 3 つの値を必要とする演算子で三項演算子とも呼ばれます。条件式の真偽に応じて二つの値を返すことができ、あたかも if 文のような処理を行うことができます。ここでは条件演算子の使い方について解説します。二項定理を確認！ （1）の解説、二項定理を使った基礎問題 （2）の解説、約分ができるので注意！定数項は？ （3）の解説、3項ある場合の考え方 （4）の解説、同じ文字がある場合は？ まとめ！ 数学の成績が落ちてきたと焦っていませんか？這個公式也稱二項式公式或二項恆等式。 使用 求和符號 ，可以把它寫作 ( x y ) n = ∑ k = 0 n ( n k ) x n − k y k = ∑ k = 0 n ( n k ) x k y n − k {\displaystyle (xy)^{n}=\sum _{k=0}^{n}{n \choose k}x^{nk}y^{k}=\sum _{k=0}^{n}{n \choose k}x^{k}y^{nk}}

高中二项式定理有理项 在数学的二项式定理中的有理项是什么意思 三人行教育网 Www 3rxing Org

二項定理 公式 三項

二項定理 公式 三項-初等代数学における二項定理（にこうていり、英 binomial theorem）または二項展開 は二項式の冪の代数的な展開を記述するものである。定理によれば、冪 n は a xb yc の形の項の和に展開できる。ただし、冪指数 b, c は b c = n を満たす非負整数で、各項の係数 a は n と b に依存して決まる特定の正整数である。例えば 2 = x 2 2 x y y 2, {\displaystyle ^{2}=x^{2}2xyy^{2},} 3 = x 3 3二項係数 二項定理の展開形は(n1)項からなる多項式となるが、 この (n1)個の項を、第0項から第n項という風に数えあげて行った場合の第r項の係数 n C r を 二項係数と呼び、

二项式定理の秒解任意项系数 知乎

二項係数のある性質 77 には単に後者をいいかえただけに過ぎない．けれども，通常の代数学 の書物では，（2）は基本的公式として書かれているが，それを定理1二項定理 まとめ 二項定理は難しい公式に見えますがその原理は実は単純です。 1150年ごろには、インドの数学者が著書 "Lilavati" で二項係数について詳しく述べている。 Hazewinkel, Michiel, ed 多項係数は二項係数の性質とよく似たたくさんの性質を満たす。それゆえに、二項級数はニュートンの（一般）二項定理とも呼ばれる。のちにニールス・アーベルは16年に『クレレ誌』に掲載された論文においてこの主題を取り上げ、特筆すべき収束問題として扱っている 。 関連項目 編集

Apr 10, 11 · 二項定理の問題なので、表記が見にくくなってしまい、すいません； nとか0とか2は、二乗とかの、全て小さいものとして表記してます； 等式（1＋X）n乗 （X＋1）n乗 ＝（1＋X）2n乗 を用いて、次の等式を証明せよ。 2y）5乗 〔x2乗y三乗〕 これに、公式のOct 13, 17 · ここでは、 xn x n を微分すると nxn−1 n x n − 1 になることを、二項定理を用いて示していきます。 ただ、当面は、出てくるものはほとんど3乗までです。 出てきても4乗です。 なので、一般の n 乗の場合を示さなくても十分やっていけます。 そのためJul 22,  · ここでは多項定理について説明します。 2項式の展開については，二項定理を利用すると，比較的楽に展開することができます。 しかし，3つ以上の項を含む多項式の累乗の展開はかなりややこしくなります。 特定の項の係数を楽に求めることができるようになるためにも，多項定理を理解して使いこなせるようにしましょう。 Contents ページ1 1 多項定理とは

Apr 15, 19 · 今まで学んだ展開公式として、中学数学で学んだ や、三乗の展開公式で学んだ といったものがあります。 次に問題となるのが、 や ですが、数字を一つずつ増やして調べていくのではきりがありませんね？ ここでは 乗の展開、つまり を計算するための方法である、二項定理についての解Dec 22, 18 · 公式の考え方は3項のときと同様です。 2 多項定理の証明（二項定理を用いる方法） すでに解説したのが多項定理の証明の1つですが、ここでは二項定理を用いた証明方法を紹介します。二項定理 要点 (ab) n を展開したとき， a n−r b r の係数は n C r になる．（ n C r を二項係数という．）

二项式定理公式妙解高考真题 颠覆你想象的解题技巧 肖博数学

高一下數學2 3a觀念01二項式定理 Youtube

Jan 13,  · 例えば式(7)においてαとβを入れ替えると、第一項と第二項が入れ替わり、第三項と第四項はそのままとなるので結局同じ式になります。 特殊な場合 式(7),(8),(9)においてα=β=γとすると三倍角の公式となります。定義 二項式は二つの単項式の和となっている多項式をいうのだから、ひとつの不定元（あるいは変数） x に関する二項式（一元二項式あるいは 一変数 （英語版） 二項式）は、適当な定数 a, b および相異なる自然数 m, n を用いて の形に書くことができる。ローラン多項式を考えている文脈さて， これら ( a b) 2 や ( a b) 3 の指数部分を n とした以下のような ( a b) n の展開公式を 二項定理と言います． 二項定理 実数 (複素数) a, b と正の整数 n に対して，次の展開公式が成り立つ． a, b は実数でも複素数でも構いません． また， n C 0 = n C n = 1 なので，以下のように a n の係数と b n の係数は1ですね． また， この 二項定理を用いて展開することを

問題二項式定理 課業板 Meteor 學生社群

A First Course In Probability Chape1 组合分析 二项式定理 在苏州的城边 博客园

定義と解釈 自然数 （ 0 も含める） n および k に対し、二項係数 (n k) は 二項冪 (1 X)n の展開における Xk の 項 の 係数 として定義できる。 同係数は（ k ≤ n のとき） 二項公式 ( x y ) n = ∑ k = 0 n ( n k ) x n − k y k {\displaystyle (xy)^ {n}=\sum _ {k=0}^ {n} {\binom {n} {k}}x^ {nk}y^ {k}} ( ∗) に現れるため「二項係数」の名がある（この式自体は 環 の互いに可換な任意の元 x, y にあるいは，次の二項定理からでも確認できる。 ∑ ∑ = = = = − = n x n x nx n x p q n C p q p x 0 0 1 ( ) ( ) (3) 「反復試行の確率」は，昔の高校数学では「独立試行の定理」と呼んだ。 T試行 を n回繰り返したとき，毎回の試行結果が他の回の試行結果に影響を重要 二項定理の公式： n C r a n−r b r において， a n−r, b r については 「係数も何乗かする」ことが重要 係数 何乗 × n C r が係数になる 負の数を奇数乗すると負の数になる．

高考数学考点之二项式定理 王羽课堂

1

三町勝久, マクドナルド多項式入門, 代数学百科i「群論の進化」朝倉書店, isbn では、p340に次のように書かれている 「あまり強調されることが ないようであるが、二項定理は数学の基本的な定理の中でも最も重要な定理であるX 2 ⋯ (1x)^ {\alpha}=1\alpha x\dfrac {\alpha (\alpha1)} {2!}x^2\cdots (1x)α = 1 αx 2!α(α − 1) x2 ⋯ を無限級数の形できちんと書くと， ( 1 x) α = ∑ k = 0 ∞ F ( α, k) x k (1x)^ {\alpha}=\displaystyle\sum_ {k=0}^ {\infty}F (\alpha,k)x^k (1x)α = k=0∑∞関わる二項定理，三項定理は，むしろ高校生の思い浮かべるものと言ってよい $(xy)^{n}= \sum_{pq=n}\frac{n!}{p!q!}x^{p}y^{q},$ $(xyz)^{n}= \sum_{pqr=n}\frac{n!}{p!q!r!}x^{p}y^{q}z^{r}$

高考压轴之二项式定理的妙用 知乎

一天一道高考題095二項式定理 每日頭條

二項定理は「組合せの考え方」を用いれば簡単に示せる。だから覚える必要はない！ 二項定理の応用例は「係数を求める」「二項係数の関係式を示す」「余りを求める(合同式)」の主に3つである。 $3$ 以上の多項になっても、基本的な考え方は変わらない。Mar 07, 21 · 一般化二項定理 ( 1 x) α = 1 α x α ( α − 1) 2!二項定理（難）問題 1104 次の式の展開式において、〔〕内の項の係数を求めよ (1) (x2y3z)^6 〔x^2y^3z〕 (2) (x^23x2)^5 〔x^3〕 (3) (2x^21/x)^6 〔定数項〕 a>0の整数とする。 (xa)^5を展開した時にx^2の係数が100を超えるためのaの最小値を求めるため、次の問い

二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ

多项式展开项系数公式 西瓜视频

場合の数9｜ 多項定理とは？ 実は 二項定理と同じ考え方！ 前々回の記事では， ( a b) n の展開公式である 二項定理について説明しました． また，前回の記事では具体的な n に対して ( a b) n の展開を計算できる パスカルの三角形について説明前回 http//googl/1vJZgA 次回 http//googl/RRbjy8サブチャンネル とある男がゲームをしてみた→http//googl/sfOiHn二項定理を簡単に覚える！ 定数項・係数の求め方 具体的な数が与えられていない整数問題でも、題意をきちんと汲んで、二項定理を使うシーンがある 次回以降のシリーズでは、二項係数のもうすこしマニアックな性質や、二項定理、二項係数の性質を利用した別の問題について扱っていきます。

高考数学考点之二项式定理 王羽课堂

二项式定理公式 搜狗百科

二項定理・三項定理の分かりやすいまとめ そうちゃ's 図解 三項定理 三項式の累乗、例えば(xyz) 9 を展開した時の「x 2 y 3 z 4 」の係数はいくつになるかを求めるのが三項定理です。 定理を導く 二項定理の「もう一つの考え方」を使えば簡単です。1665年ごろアイザック・ニュートンは定理を一般化して非整数冪に対する公式（ニュートンの一般二項定理）を得た 。 この一般化において、有限和は無限級数で置き換えられなければならない。 またこの一般化を行うために二項係数 (テンプレートSu) の上の添字 n を任意の値としなければならNov 21, 09 · 二項定理の問題がわかりません。詳しく簡単におしえてください。おねがいします。 nは2以上の整数とする。二項定理を利用して、次のことを示せ。 (1) a＞0のとき （1＋a）^n＞1＋na (2) (1＋1/n)^n＞2 よろしくおねがいします。

笔记 排列组合公式 二项式定理 Coke的博客 Csdn博客 二项式定理公式

二项式定理 搜索结果 哔哩哔哩 Bilibili

Apr 21,  · 二乗、三乗の二つだけなのです。以下に注意点として載せておきます。 要注意あくまで推測の世界。一般化は「二項定理」で。 注意点としては、 あくまで「 三乗の展開公式 」「 二乗の展開公式 」 にのみ 共通する規則性であるということです。Jun 06, 21 · 二項定理は，二項に関する定理ですから， (ab)とか， (xy)のように，２つの「項」がある式を相手にしています。 もちろん，3x4yや，a 2 3bcという式も「二項」です。 (ab)の1乗はabです。 (ab)の2乗はa 2 2abb 2 です。Jan 22, 19 · 二項定理を導出する では公式を作りましょう。 といってもどうしたら良いでしょうか。 もちろん一個一個確認するなんてやり方はできませんのでうまい方法を考えなくてはなりません。 まず一番最初に考えた 2 乗の展開から考えてみます。 これを一個

高考小题 二项式定理の十秒搞定常数项 知乎

二項式定理 維基百科 自由的百科全書

1665年ごろアイザック・ニュートンは定理を一般化して非整数冪に対する公式（ニュートンの一般二項定理）を得た 。 この一般化において、有限和は無限級数で置き換えられなければならない。 またこの一般化を行うために二項係数 (n k) の上の添字 n を任意の値としなければならないから、二3乗の因数分解（展開）公式 2919k件のビュー 19年版模試日程まとめ（河合塾・駿台・東進・代ゼミ） 27k件のビュー 3x4yや，aが用いられている。 冪指数 α が自然数 n のときは、上記の級数の n 2 番目以降の項はすべて零になる（明らかに、各項の因子に n − n が現れる）から、このとき級数は有限和であって、代数的な二項定理が導出される。;

二项式定理概念公式称为二项式定理 二项式系数各项的系数c N R R 0 1 2 N 二项式通项c N R A N

Ppt 二項式定理powerpoint Presentation Free Download Id

Nov 16, 18 · 二項定理 応用 三角函数の多倍角公式複素数に対する二項定理とド・モアブルの定理を合わせれば、正弦函数および余弦函数の多倍角公式が得られる。ド・モアブルの公式によれば cos ⁡ (3項以上の式の展開 3つ以上の項がある式に二項定理をどうやって使うのか。 ここではその方法を紹介します。 例えば、 これの展開にそのまま二項定理を使うことはできません。 二項定理とは、その名の通り、2つの項を展開するときの定理ですからね。Dec 21, 18 · 1 二項定理とは？ それではさっそく二項定理の公式について解説していきます。 11 二項定理の公式 二項定理 \( \color{red}{ \begin{align} (ab)^n = & {}_n \mathrm{C}_0 a^n b^0 {}_n \mathrm{C}_1 a^{n1} b^1 \\ & {}_n \mathrm{C}_2 a^{n2} b^2 \cdots \\ & {}_n \mathrm{C}_r a^{nr} b^r \cdots \\

1x版高中数学第一章计数原理习题课二项式定理的应用学案苏教版选修2 3下载 Word模板 爱问共享资料

二项式定理典型例题 Doc 沃文网wodocx Com

Apr 11, 18 · 二項定理の公式にC (コンビネーション)が出てくる理由 となっています。 これはaの三乗を作るためには (ab) (ab) (ab)の中からa掛けるa掛けるaを 選び出す しか無く、その 場合の数を求める為にCを使っている のです。 この場合では1通りなので (1)・ (a^3)となっています。 同様に、 a 2 bの係数を考えると、（ab) (ab) (ab)から、aを2つとbを1つ選ぶ場合の数を証明は 二項係数の和，二乗和，三乗和 ∑ k = 0 n p C k ⋅ q C n − k = p q C n \displaystyle\sum_{k=0}^n{}_p\mathrm{C}_k\cdot {}_q\mathrm{C}_{nk}={}_{pq}\mathrm{C}_n k = 0 ∑ n p C k ⋅ q C n − k = p q C nΣシグマの公式まとめと計算方法（数列の和の公式） 4984k件のビュー 数列漸化式の解き方10パターンまとめ 3676k件のビュー;

牛頓的數學成就 之一 二項式定理 雪花新闻

二项式定理 高中数学知识点 高考圈

Apr 10, 17 · 二項定理の有名な公式を解説！ ここでは、大学受験で使える二項定理の有名な公式を3つ説明します。 「何かを選ぶということは、他を選ばなかったということ」 まずはこちらの公式。 文字のままだとわかりにくい方は、数字を入れてみてください。 6c4 = 6c2二項冪、すなわち二項式 x y の n乗 (x y) n は二項定理（あるいは同じことだがパスカルの三角形）の意味するところによって展開することができる。例えば、二項式 x y の平方は、各々の項の平方と互いの項の積の二倍との和に等しい (x y)^2 = x 2 2xy y 2

高中二项式定理有理项 在数学的二项式定理中的有理项是什么意思 三人行教育网 Www 3rxing Org

高考数学考点之二项式定理 王羽课堂

Q Tbn And9gcq C0fymrzcg 9aaq1py1tdo6e4x57gaguluvpzejt3gwayavjc Usqp Cau

高中数学之排列 组合定义及二项式定理 段智华的博客 Csdn博客

A First Course In Probability Chape1 组合分析 二项式定理 在苏州的城边 博客园

二项式定理 Geogebra

二项式定理の秒解任意项系数 知乎

二项式定理公式妙解高考真题 颠覆你想象的解题技巧 肖博数学

4 二項式定理例題3 Youtube

2 4二項式定理

二項式定理 翰林雲端學院

二項式定理 維基百科 自由的百科全書

聚焦 二项式定理 中的思维方法 附同步真题

高中二项式定理有理项 在数学的二项式定理中的有理项是什么意思 三人行教育网 Www 3rxing Org

二項定理の基本 Youtube

数ii 二項定理 3項のn乗 Youtube

二項定理ってなんだよ 多項定理ってなんだよ ってなっている君へ

版高中数学第一章计数原理习题课二项式定理的应用学案苏教版选修2 3 莲山文库

二项式定理 学习视频教程 腾讯课堂

Word如何输入数学中 二项式定理 公式 百度经验

二項式定理原理及其範例 Youtube

二项式定理 维基百科 自由的百科全书

03 二项式系数与系数和 二项式定理高中数学 Youtube

二项式定理教案

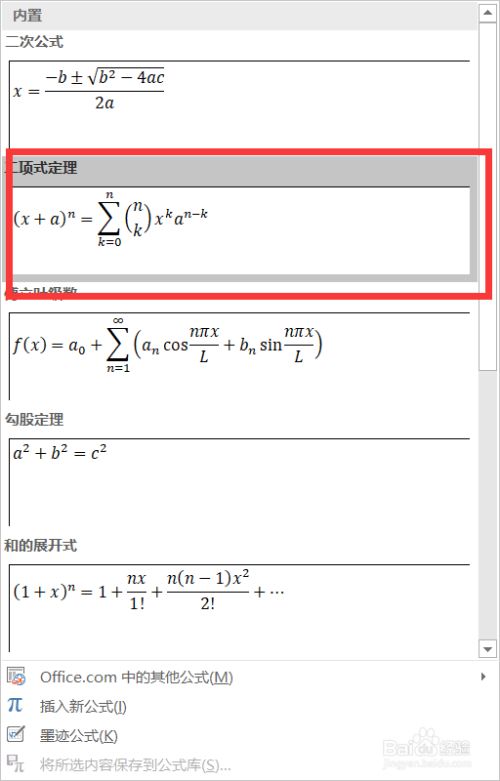
Word如何输入数学中 二项式定理 公式 百度经验

二項式定理 維基百科 自由的百科全書

二项式定理知识点总结下载 Word模板 爱问共享资料

二項式定理 維基百科 自由的百科全書

组合数学及其应用 二项式定理 在苏州的城边 博客园

利用杨辉三角形来解释二项式定理 多项式 展开式 网易订阅

二项式定理典型例题下载 Word模板 爱问共享资料

5 1 二项式定理 新闻 蛋蛋赞

二項式 二項式是隻有兩項的多項式 即兩個單項式的和 是僅次于單項式的最簡單多項式 華人百科

杨辉三角 与 二次项定理 的相遇 成就了数学史上的一段美谈

Word如何输入数学中 二项式定理 公式 百度经验

二项式定理 题型有求系数 求特项 会赋值等 真题解析 高中数学 学习资料大全 免费学习资源下载

二项式定理公式妙解高考真题 颠覆你想象的解题技巧 肖博数学

二项式的展开式的常数项定理 哔哩哔哩 つロ干杯 Bilibili

Ggakckocbwxr4m

高考压轴之二项式定理的妙用 知乎

二項式係數 维基百科 自由的百科全书

二項式定理

二項式定理的十種題型及解決 人人焦點

5 1 二项式定理 新闻 蛋蛋赞

第二部分运算 代数第四章字母与代数式首都师范大学王尚志 第四章字母与代数式字母与代数式的功能 字母替代数的作用符号的分类与作用多项式运算 代数和与合并同类项乘积 公式 二项式定理除 余数定理

二项式定理的系数cnk怎么求 百度经验

二项式定理の秒解任意项系数 知乎

Wf1jsddslx3abm

一看就懂的二项式定理 三项式 多项相乘秒杀大招 哔哩哔哩 つロ干杯 Bilibili

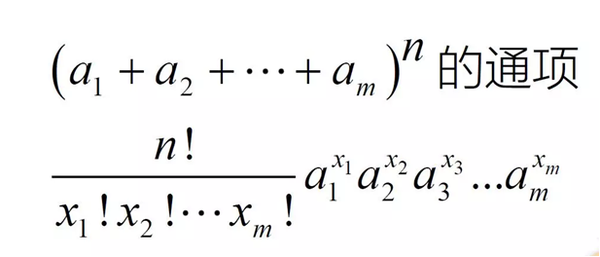
什么 多项式定理都不会 从此三项式秒杀 知乎

一招破解高中數學二項分佈與超幾何分佈 雪花新闻

二項式定理 二項式定理 英語 Binomial Theorem 又稱牛 華人百科

5 1 二项式定理 新闻 蛋蛋赞

二項式定理 二項式定理 英語 Binomial Theorem 又稱牛 百科知識中文網

二项式定理与杨辉三角 玄数

二项式求常数项题型 高中数学二项式定理中 二项式系数 系数 常数项分别是什么 求解答 三人行教育网 Www 3rxing Org

二項定理を簡単に覚える 定数項 係数の求め方 高校数学の知識庫

高中数学经典解题方法大全 二项式定理三种常见考题精妙解题方法 学习

二項式定理 Youtube

组合数学及其应用 二项式定理 在苏州的城边 博客园

二项式系数 快懂百科

二项式的展开式的常数项定理 哔哩哔哩 つロ干杯 Bilibili

二项式定理展开式二项式定理经典例题 二项式定理公式大全

排列組合二項式定理給一等比多項式連加求某一項係數要利用等比級數合的公式填充永平段考 Youtube

二项式定理 搜狗百科

高中数学知识点 二项分布 高二知识点总结 求学网

Word如何输入数学中 二项式定理 公式 百度经验

二项式定理 简书

澳門四校聯考數學攻略組 和常數有關的二項式定理 17年出了一次 年又一次 下次不會再有了吧 Facebook

1

1

二项式定理 高中数学知识点 高考圈

高考压轴之二项式定理的妙用 知乎

高中數學必修五 二項式定理突破點 一 二項式的通項公式及應用 每日頭條

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

组合数学及其应用 二项式定理 在苏州的城边 博客园

1x 19年高中数学第一章计数原理1 3 1 二项式定理学案新人教a版选修2 3下载 Word模板 爱问共享资料

二项式定理公式推导 技术成就梦想 梦想成就未来 Csdn博客 二项式定理的推导

二項式定理 維基百科 自由的百科全書

二項式定理 維基百科 自由的百科全書

選修2 3 高中數學必備知識點 1 4二項式定理 雪花新闻

牛頓的二項式定理 上 線代啟示錄

Incoming Term: 二項定理 公式 三項,